Optimización de Cartera

Configuraciones Iniciales

Antes de comenzar con nuestra optimización de cartera, utilizando la teoría del portafolio de Markowitz, designaremos las configuraciones iniciales para el trabajo, comenzando con la verificación, instalación y carga de los paquetes a utilizar para el caso, luego de ello, al mismo tiempo hacemos unas configuraciones aparte para el entorno de trabajo propiamente tal (no es necesario para el markdown, sin embargo, para aquellos que quieran replicar el modelo, les sea útil), con esto todo

knitr::opts_chunk$set(echo = TRUE, include = TRUE, fig.align = "center",fig.width = 8.5, fig.height = 9, message = FALSE, warning = FALSE)
#############################################################################
# Portfolio Opimization
# Author: Matías Vicuña Cofré
#############################################################################
#******************** Configuraciones e Inicializacion *********************#
#############################################################################
{
  # Librerías
  {
    # Lista de paquetes que quieres verificar
    paquetes <- c("tidyverse","janitor","skimr","scales","ggthemes",
                  "tseries","fPortfolio","knitr","kableExtra","gplots",
                  "plotly", "lubridate","gplots","formattable","qrmtools")
    
    # Verificar e instalar paquetes que no estén instalados
    for (paquete in paquetes) {
      if (!require(paquete, character.only = TRUE)) {
        install.packages(paquete)
      }
    }
    remove(paquetes)
    
    # Activacion Librerias
    suppressPackageStartupMessages({
      library(tidyverse) # Nucleo de trabajo
      library(janitor) # Ajustes para data frames
      library(skimr) # Estadísticas de datos detalladas
      library(scales) # Ajuste de escalas (principalmente en ggplot2)
      library(ggthemes) # Temas para ggplot2
      library(tseries) # Transformación y uso de formato "ts", "zoo", etc
      library(fPortfolio) # Optimización de Cartera
      library(knitr) # Ajustes para tablas (junto con formattable)
      library(kableExtra) # Complemento de knitr
      library(plotly) # Gráficos Interactivos
      library(lubridate) # Ajustes de Fechas
      library(gplots) # Mapa de calor
      library(formattable) # Tablas HTML
      library(qrmtools) # Para calculos de rendimientos
    })
  }
  # Configuraciones Entorno de Trabajo
  {
    # Limpiamos el entorno de trabajo
    rm(list = ls())
    
    # Limpiamos la Memoria (RAM)
    gc(reset = TRUE)
    
    # Limpiamos la consola
    cat("\014")
    
    # De número científico a natural
    options(scipen = 999)
  }
}

---

Indicador de Mercado y Tasa libre de Riesgo

S&P 500

Luego de las configuraciones, generamos la primera muestra de datos a utilizar, usando el paquete tseries, como primer ejemplo, utilizaremos el índice S&P 500 Dow Jones, al cuál observaremo su precio histórico desde Enero del 2000 hasta el 31 de diciembre del 2023, usaremos su ticket de Yahoo Finance (^GSPC) (veáse más detalle del índice aquí).

Junto con ello, usamos el paquete skimr para realizar un análisis estadístico básico de la serie con los precios históricos, teniendo su media, percentiles y demás detalles.

# Preambulo (Rango de fechas a considerar para medición)
start_port <- as.Date("2000-01-01")
end_port <- as.Date("2023-12-31")
quote_port <- "AdjClose"

# Carga serie S&P 500.
SP500 <- get.hist.quote(
  instrument = "^GSPC",
  start = start_port,
  end = end_port,
  quote = quote_port,
  quiet = TRUE
)

# Renombramos la base original
colnames(SP500) <- "SP500"

# Ajustamos la muestra
SP_500 <- SP500 %>%
  as_tibble() %>% 
  mutate(Fecha = as_date(time(SP500))) %>% 
  rename(Precio = SP500)

# Generamos tabla resumen de precios históricos
formattable(skim_without_charts(SP_500$Precio))

skim_type	skim_variable	n_missing	complete_rate	numeric.mean	numeric.sd	numeric.p0	numeric.p25	numeric.p50	numeric.p75	numeric.p100
numeric	data	0	1	1973.587	1061.336	676.53	1191.38	1457.34	2584.84	4796.56

Ya teniendo la serie cargada, generamos ahora un pequeño gráfico que entrega el rendimiento histórico desde el 2000 al 2023 del precio ajustado del indicador.

Para ello, hacemos uso de un recursos super relevantes para el análisis y visualización de datos: ggplot2, con este paquete y usando de adicional para la interacción el paquete plotly, tenemos un gráfico que nos entrega en detalle e intuitivamente el desarrollo de este mercado Norteamericano.

# Generamos el gráfico
int_plot_SP500 <- SP_500 %>%
  ggplot(mapping = aes(x = Fecha,
                       y = Precio)) +
  geom_line(aes(y = Precio),
            color = "blue4") +
  labs(x = "Años",
       y = "Precio $USD",
       title = "Precio Ajustado S&P 500") +
  
  theme_minimal() +
  theme(axis.title.x = element_text(size = 12, 
                                    face = "bold"),
        axis.title.y = element_text(size = 12, 
                                    face = "bold"),
        plot.title = element_text(size = 20,
                                  face = "bold", 
                                  hjust = 0.5))

# Generamos el gráfico de forma interactiva
ggplotly(int_plot_SP500)

Bono del Tesoro Norteamericano

Además de tener los datos de este índice de mercado norteamericano, necesitamos tener un instrumento que, siguiendo la teoría de Markowitz, sea el que simule nuestro rendimiento “libre de riesgo” (risk free), de este modo, y siguiendo la dinámica de este ejercicio, usaremos el Treasury Yield 30 Years, el cuál será nuesrtro indicador histórico que seguirá la idea de tasa “segura” de ganar. Este indicador, al igual que todos los demás, son recuperados directamente desde

# Cargamos los datos desde Yahoo Finance
riskfree <- get.hist.quote(instrument = "^TYX",
                            start = start_port, 
                            end = end_port,
                            quote = quote_port,
                            quiet = TRUE
                            )

# Cambiamos el nombre de la columna
colnames(riskfree) <- "RiskFree"

# Ajustamos la muestra
risk_free <- riskfree %>%
  as_tibble() %>% 
  mutate(Fecha = as_date(time(riskfree))) %>% 
  rename(Tasa = RiskFree)

# Estadística Descriptiva de los datos
formattable(skim_without_charts(risk_free$Tasa))

skim_type	skim_variable	n_missing	complete_rate	numeric.mean	numeric.sd	numeric.p0	numeric.p25	numeric.p50	numeric.p75	numeric.p100
numeric	data	1329	0.8194048	3.832461	1.1775	0.937	2.93125	3.8415	4.781	6.742

# Generamos el gráfico
int_plot_risk_free <- risk_free %>%
  na.omit() %>% 
  ggplot(mapping = aes(x = Fecha,
                       y = Tasa)) +
  geom_line(aes(y = Tasa),
            color = "red4") +
  labs(x = "Años",
       y = "Tasa rendimiento",
       title = "Bono del Tesoro de EE.UU. a 30 años") +
  
  theme_minimal() +
  theme(axis.title.x = element_text(size = 12, 
                                    face = "bold"),
        axis.title.y = element_text(size = 12, 
                                    face = "bold"),
        plot.title = element_text(size = 18,
                                  face = "bold", 
                                  hjust = 0.5))

# Generamos el gráfico de forma interactiva
ggplotly(int_plot_risk_free)

---

Consolidando la cartera

Siguiendo con esta ídea, ahora generaremos una cartera, la cuál se compondrá de a lo menos 7 tipos de empresas, para este ejemplo, usaremos empresas que cotizan en la bolsa de Nueva York, especificamente serán las siguientes:

• Coca Cola (KO)
• Pepsi Cola (PEP)
• Walmart (WMT)
• Target (TGT)
• Apple (AAPL)
• Microsoft (MSFT)
• Amazon (AMZN)

Con este listado de empresas, ahora construiremos nuestra base.

# Datos Previos
tickets <- c("KO", "PEP", "WMT", "TGT", "AAPL", "MSFT", "AMZN")
portafolio <- tibble()

# Iteración de Recopilación de Series
for (i in seq_along(tickets)) {
  data <- get.hist.quote(
    instrument = tickets[i],
    start = start_port,
    end = end_port,
    quote = "Adjusted",
    quiet = TRUE
  )

  # Verifica si el objeto portafolio está vacío
  if (nrow(portafolio) == 0) {
    portafolio <- data
  } else {
    # Combina las series temporales por columna
    portafolio <- cbind(portafolio, data)
  }
}

# Asigna nombres de columna al portafolio
colnames(portafolio) <- tickets

# Extraemos la fecha de la base (para gráficar)
Fecha <- time(portafolio)

# Imprime el resultado
rmarkdown::paged_table((cbind(format(Fecha, "%d-%m-%Y"),as_tibble(portafolio))))

Teniendo ya conformada la cartera, visualizamos la evolución histórica de cada serie

# Creamos un reshape "wide to long" para facilitar la graficación
portafolio_long <- cbind(Fecha,as_tibble(portafolio)) %>%
  gather(key = "Ticket", value = "Precio", -Fecha)

# Creamos el gráfico de series de tiempo
int_plot_portafolio <- ggplot(portafolio_long, 
                              aes(x = Fecha, y = Precio, group = Ticket, color = Ticket)) +
  geom_line(aes(y = Precio)) +
  facet_wrap(~Ticket, scales = "free_y") +
  labs(title = "Evolución Histórica",
       x = "Fecha", y = "Precio $USD") +
  scale_color_calc() +
  theme_minimal() +
  theme(axis.title.x = element_text(size = 15, face = "bold"),
        axis.title.y = element_text(size = 15, face = "bold"),
        plot.title = element_text(size = 20, face = "bold", hjust = 0.5),
        axis.text.x = element_text(face = "bold", vjust = 1),
        legend.position = "none")
  
# Agregamos la interacción
ggplotly(int_plot_portafolio)

Posterior a esto, crearemos los beneficios de cada serie (incluida el S&P 500 y el bono del tesoro), añadiendo además una normalización logartímica para reescalar la muestra.

Retornos para cada serie

# Calculamos los rendimientos de la cartera
returns_portafolio <- round(returns(portafolio, method = "logarithmic"), digits = 4)

# Calculamos los rendimientos del indice S&P 500
aux_SP500 <- returns(SP500, method = "logarithmic")
returns_SP500 <- aux_SP500 %>% 
  as_tibble() %>% 
  rename(SP500 = V1)
returns_SP500 <- xts::reclass(returns_SP500,match.to = aux_SP500)

# Calculamos los rendimientos del Bono del Tesoro
aux_riskfree <- returns(riskfree, method = "logarithmic")
returns_riskfree <- aux_riskfree %>% 
  as_tibble() %>% 
  rename(riskfree = V1)
returns_riskfree <- xts::reclass(returns_riskfree,match.to = aux_riskfree)

# Imprimimos los resultados 
aux_data_printed <- merge(returns_portafolio,round(returns_riskfree,digits = 4),round(returns_SP500, digits = 4))
Date <- time(aux_data_printed)
Date <- format(Date, "%d-%m-%Y")
rmarkdown::paged_table(cbind(Date,as_tibble(aux_data_printed)))

Gráficamente esto se ve de la siguiente manera:

# Ajustes a la muestra (formateo de zoo a tibble)
data_long <- merge(returns_portafolio,returns_SP500,returns_riskfree)
Time <- time(data_long)

# Creamos un reshape "wide to long" para facilitar la graficación
data_long <- cbind(Time,as_tibble(data_long)) %>%
  gather(key = "Serie", value = "Precio", -Time)

# Creamos el gráfico de series de tiempo
int_plot_data_long <- ggplot(data_long, 
                              aes(x = Time, 
                                  y = Precio, 
                                  group = Serie, 
                                  color = Serie)) +
  geom_line(aes(y = Precio)) +
  facet_wrap(~Serie, scales = "free_y") +
  labs(title = "Variación Precios Histórica Normalizada",
       x = "Fecha", y = "Precio $USD") +
  scale_color_calc() +
  theme_minimal() +
  theme(axis.title.x = element_text(size = 13, face = "bold"),
        axis.title.y = element_text(size = 13, face = "bold"),
        plot.title = element_text(size = 18, face = "bold", hjust = 0.5),
        axis.text.x = element_text(face = "bold", vjust = 1),
        legend.position = "none")
  
# Agregamos la interacción
ggplotly(int_plot_data_long)

---

Análisis Estadístico Inicial

Posterior a tener las variaciones diarias de cada serie, procedemos a generar los rendimientos promedios, desviación, varianza, covarianza y correlación de las series respectivamente

# Promedios Rendimientos
promedio <- round(sapply(returns_portafolio,mean), digits = 6)

# Varianza Rendimientos
varianza <- round(sapply(returns_portafolio, var), digits = 6)

# Desviación Rendimientos
desviacion <- round(sapply(returns_portafolio, sd), digits = 6)

# Matriz de Varianzas y Covarianzas
covarianzas <- round(cov(returns_portafolio), digits = 6)

# Matriz de Correlación
correlacion <- round(cor(returns_portafolio) * 100, 2)

# Imprimimos los resultados de Promedio, Varianza y Desviación
recuadro <- rbind(promedio,varianza,desviacion)
formattable(as_tibble(recuadro, rownames = NA))

	KO	PEP	WMT	TGT	AAPL	MSFT	AMZN
promedio	0.000232	0.000351	0.000212	0.000303	0.000899	0.000388	0.000585
varianza	0.000171	0.000159	0.000220	0.000429	0.000656	0.000371	0.000971
desviacion	0.013067	0.012605	0.014817	0.020717	0.025609	0.019251	0.031166

Teniendo la información estadística relevante, ahora finalizamos el análisis previo con un mapa de calor, el cuál visualiza la correlación que posee cada una de las series de nuestra muestra, siendo los sectores más rojizos aquellos que se alejan de la correlación positiva (\(\rho<1\)), mientras que las zonas más amarillas o anaranjadas corresponden a una correlación entre ellas mayor (\(\rho\sim1\)). Para una mayor comprensión y simplicidad del análisis, transformamos en la chunck anterior la correlación entre las series, siendo estas multiplicadas por 100, de este modo en el gráfico el valor que representa cada recuadro corresponde a su correlación porcentual.

generate_heat_map <- function(correlationMatrix, title)
{
  heatmap.2(
    x = correlationMatrix,
    cellnote = correlationMatrix,
    main = title,
    symm = TRUE,
    dendrogram = "none",
    Rowv = FALSE,
    trace = "none",
    density.info = "none",
    notecol = "black",
    key.title = "Nivel Correlación",
    key.xlab = ""
  )
}

generate_heat_map(correlacion, "Mapa Correlación Cartera")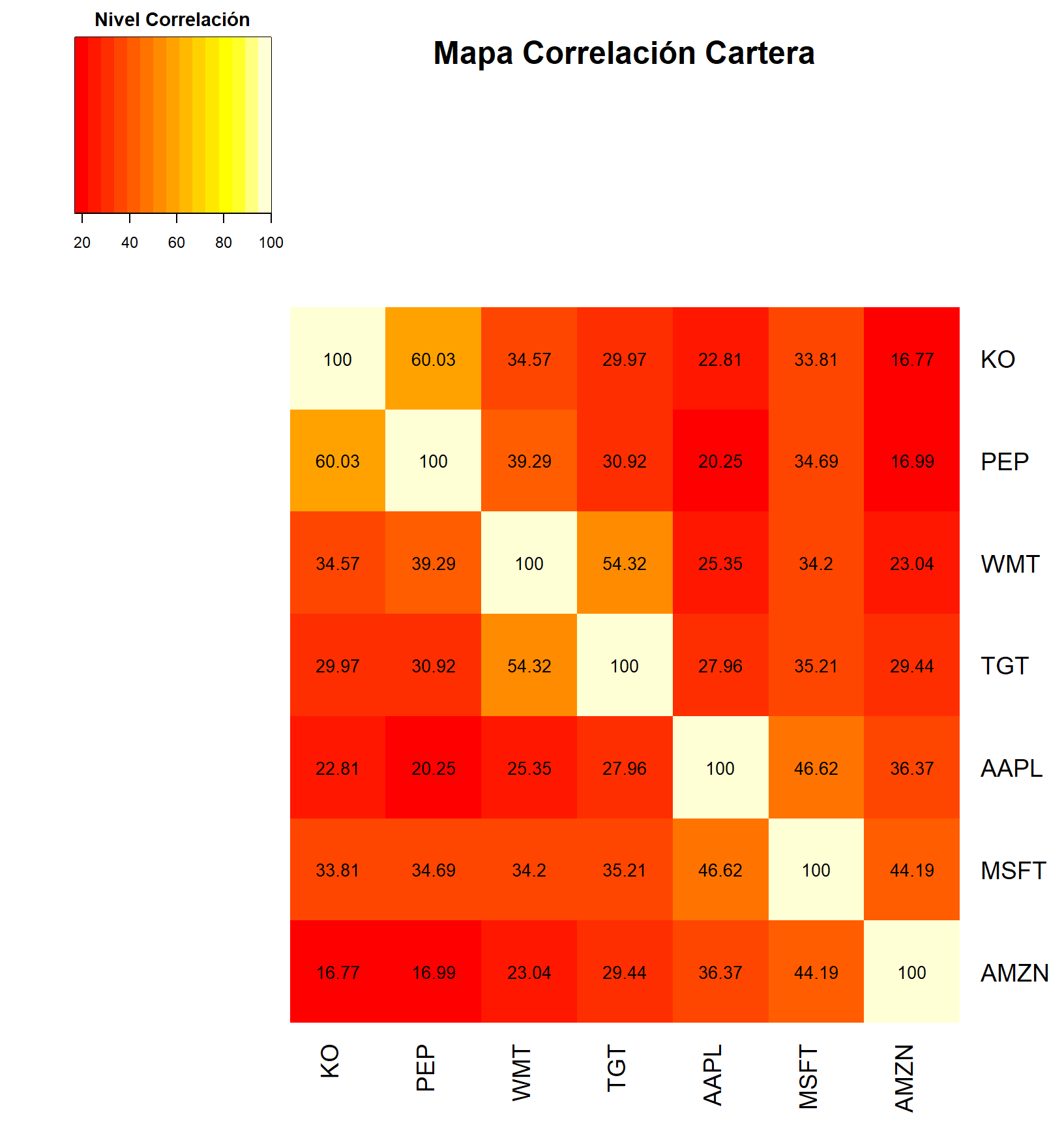

Con este análisis previo tenemos la siguiente información

---

El Modelo

# Especificaciones del Modelo
markov <- portfolioSpec() # Generamos las especificaciones
constraints <-  "Shorts"  # Determinamos la restricción a "venta corta"

# Determinamos la tasa libre de riesgo del Modelo
setRiskFreeRate(markov) <- as.numeric(mean(returns_riskfree, na.rm = TRUE))

# Seteamos el número de portafolios a simular en la frontera eficiente
setNFrontierPoints(markov) <- 50

# Calculamos el Modelo de Markowitz de Mínima Varianza
Frontera <-
  portfolioFrontier(as.timeSeries(returns_portafolio), 
                    spec = markov, 
                    constraints)

# Imprimimos los resultados
print(Frontera)

## 
## Title:
##  MV Portfolio Frontier 
##  Estimator:         covEstimator 
##  Solver:            solveRquadprog 
##  Optimize:          minRisk 
##  Constraints:       Short 
##  Portfolio Points:  5 of 50 
## 
## Portfolio Weights:
##        KO    PEP    WMT    TGT   AAPL   MSFT   AMZN
## 1  0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000
## 13 0.2116 0.4272 0.1768 0.0027 0.1307 0.0221 0.0288
## 25 0.0000 0.6082 0.0019 0.0000 0.3394 0.0000 0.0505
## 37 0.0000 0.3088 0.0000 0.0000 0.6497 0.0000 0.0415
## 50 0.0000 0.0000 0.0000 0.0000 1.0000 0.0000 0.0000
## 
## Covariance Risk Budgets:
##        KO    PEP    WMT    TGT   AAPL   MSFT   AMZN
## 1  0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000
## 13 0.1889 0.4182 0.1553 0.0025 0.1798 0.0223 0.0331
## 25 0.0000 0.4176 0.0009 0.0000 0.5281 0.0000 0.0534
## 37 0.0000 0.0863 0.0000 0.0000 0.8830 0.0000 0.0307
## 50 0.0000 0.0000 0.0000 0.0000 1.0000 0.0000 0.0000
## 
## Target Returns and Risks:
##      mean    Cov   CVaR    VaR
## 1  0.0002 0.0148 0.0346 0.0213
## 13 0.0004 0.0108 0.0253 0.0162
## 25 0.0005 0.0133 0.0309 0.0199
## 37 0.0007 0.0184 0.0418 0.0271
## 50 0.0009 0.0256 0.0574 0.0371
## 
## Description:
##  Fri Feb  9 04:12:51 2024 by user: matias

# Generamos el Gráfico de nuestra simulación
frontierPlot(Frontera)
grid()
tangencyPoints(Frontera,
               pch = 19,
               col = "red",
               cex = 2)
tangencyLines(Frontera,
              col = "grey",
              pch = 19,
              cex = 2)
minvariancePoints(Frontera,
                  col = "blue",
                  pch = 19,
                  cex = 2)
monteCarloPoints(Frontera,
                 mCsteps = 10000,
                 col = "#0098D5",
                 cex = 0.001)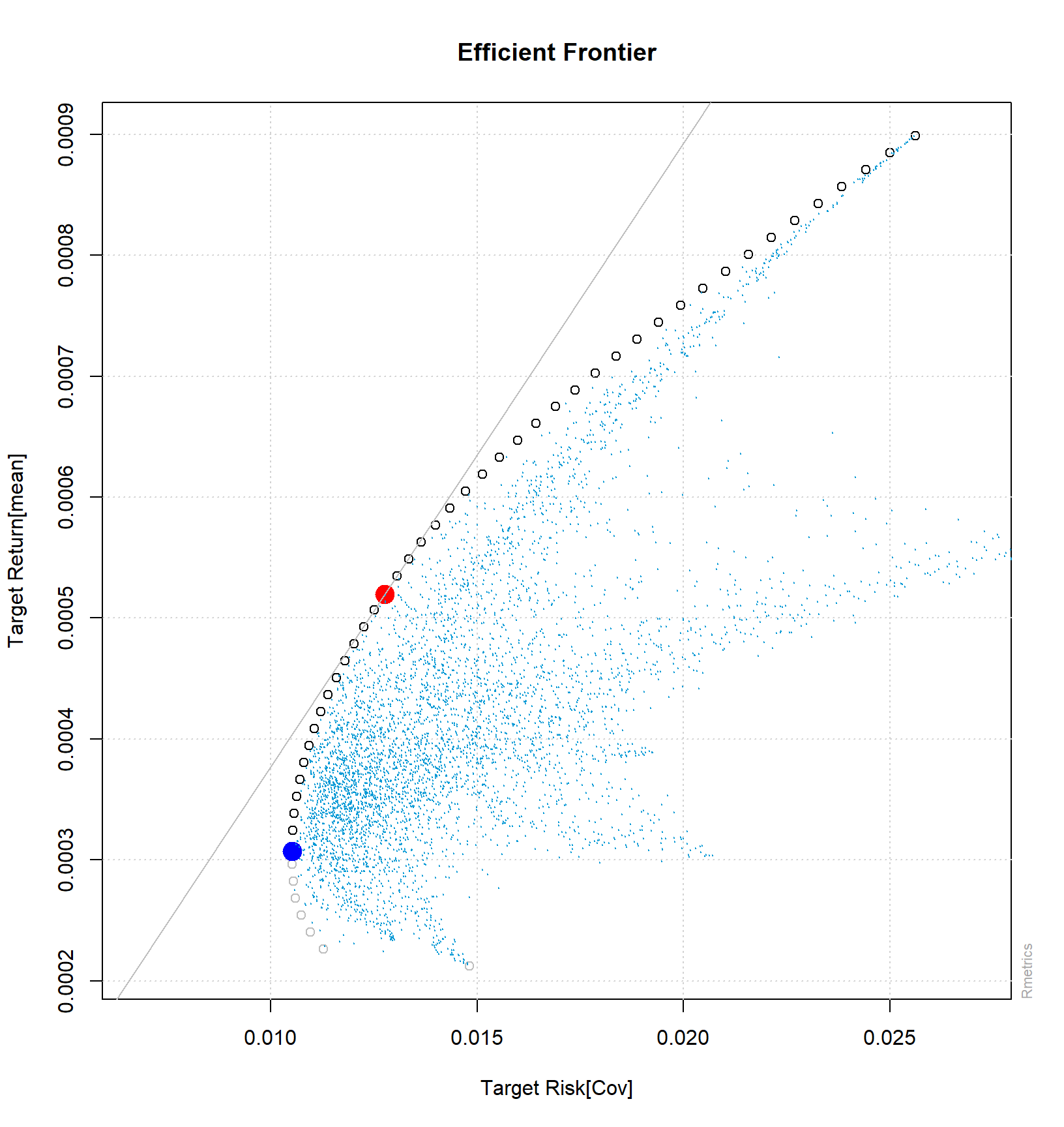

---

Copyright © 2024 Matías Vicuña Cofré, Todos los Derechos Reservados.